Research Program

Carbon, with its unique binding properties, is the element in the periodic table that provides the basis for life on earth. It is the key for many technological applications that range from drugs to synthetic materials and that have become indispensable in our modern civilization. The reason for this outstanding role is the ability of carbon to bind to itself and to almost any other element in a nearly limitless variety of ways. The resulting structural diversity of organic molecules and compounds is accompanied by a broad range of chemical and physical properties. The tools of modern synthetic chemistry allow tailored designing these properties almost at will via the controlled combination of structure- and function-defining building blocks in new target systems. Elemental carbon exists in two natural allotropes, diamond and graphite that consist of extended networks of sp³– and sp²­-C-atoms, respectively. These two forms exhibit a number of unique physical properties such as hardness, thermal conducti­vity, lubrication behavior, and electrical conductivity, which have made them attractive for many industrial applications.

Conceptually, many other ways to construct carbon allotropes besides diamond and graphite are possible upon altering the periodic binding motif in networks consisting of sp³-, sp²– and sp-hybridized C-atoms.^[1] As a consequence of the remarkable physical properties expected of these so-far elusive carbon allotropes, it has been appealing for quite some time to develop concepts for their preparation in macroscopic quantities. However, diamond and graphite represented the only known allotropes of carbon through centuries of scientific research. This situation changed in 1985,^[2] with the advent of the fullerenes (Figure 1), whose production in macroscopic quantities succeeded in 1990.^[3] The discovery of the fullerenes was awarded with the Nobel Prize for Chemistry in 1996 and marked the beginning of an “era of synthetic carbon allotropes”.^[4] The next representatives of this growing family are the carbon nanotubes (1991)^[5] and graphene (2004)^[6] (Figure 1).

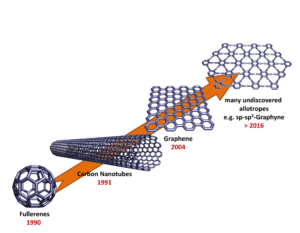
The isolation and characterization of graphene was recognized by the award of the Nobel Prize in Physics in 2010. Keeping in mind the numerous possible carbon modifications and the general interest in investigating this challenge, doubtless, further revelations are waiting.

The fullerenes, with C₆₀ as most prominent and abundant representative, are molecular carbon allotroppes. They consist of a spherical or spheroid network of sp²-C-atoms.^[7] Apart from hexagonal rings, which also represent the smallest repetition unit of planar graphite sheets, exactly 12 pentagons must be incorporated in a fullerene structure to provide the curvature required for the spherical closure of the carbon network. The 12 pentagons of C₆₀ are surrounded by 20 hexagons, as a consequence of the isolated pentagon rule (IPR).

The resulting l_h-symmetrical truncated icosahedron has the shape of a soccer ball, consisting of 60 structurally equivalent C-atoms. C₆₀ is the smallest stable fullerene. Many representatives of higher fullerenes such as D_5h-C₇₀, chiral D₂-C₇₆ and D_6h-C₈₄ have been isolated and structurally characterized. ^[7] A second family of fullerenes, formed by the condensation of evaporated carbon, are endohedral fullerenes incorporating guest atoms or molecules in the interior of the carbon framework. ^[7] Examples are La@C₈₂ and Sc₃N@C₈₀.

Soon after the discovery of the fullerenes, the formation of the quasi 1-dimensional carbon nanotubes from evaporated graphite was reported.^[5] Depending on the preparation conditions, either single (SWNTs) or multi-walled carbon nanotubes (MWNTs) are obtained. Carbon nanotubes can be considered as seamless rolled-up graphite sheets.^[8] The corresponding tubular networks of bent sp²-C-atoms are characterized by a pronounced 1-dimensionality because of their very high aspect ratios. Typical diameters of SWNTs are in the range of 1-2 nm, whereas the lengths can easily reach values in the millimeter regime and beyond. Current production methods for carbon nanotubes lead to the formation of mixtures of tubes with many different helicities, which are characterized by the so called m,n-values of the roll-up vectors.

The youngest representative of synthetic carbon allotropes is 2-dimensional graphene, which is a single sheet of graphite. Graphene, mother of all expanded aromatic carbon modifications, had for a very long time been considered a material accessible exclusively to theoretical studies. The first groundbreaking physical experiments regarding the 2-dimensional allotrope graphene succeeded in 2004,^[6] based on a simple mechanical exfoliation of graphite using Scotch® tape. Within these three families of synthetic carbon allotropes, graphene is the structurally most uniform macromolecular form in which only the sheet extensions and nature of edges can differ.

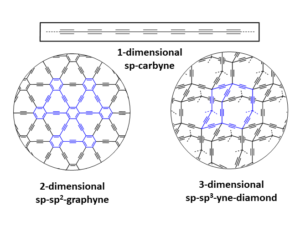
During the investigation of these sp²-allotropes attention has also been paid towards the development of other new synthetic carbon allotropes.^{[1, 9]} The extension of the construction principle by allowing sp- and sp³-C-atoms also to be incorporated into carbon networks offers almost limitless structural possibilities and opportunities (Figure 2).

The simplest example for such synthetic carbon allotropes is 1-dimensional carbyne, which consists of infinite chains of sp-C-atoms. Whereas the parent allotrope itself is still elusive, a number of model compounds, e.g. endcapped polyynes, have been synthesized and characterized. The combination of sp-, sp²– and sp³-C-atoms leads to many possible 2- and 3-dimensional carbon allotropes, of which only graphyne and graphdiyne have received any serious synthetic attention.^[9c] Significant molecular segments of graphyne and graphdiyne have been synthesized, and their study suggests attractive optoelectronic and self-assembly properties. Allotropes with a skeleton of sp- and sp³-hybridized carbon are the least studied class of hybrid allotropes, and the only notable example thus far reported is expanded cubane.^[9c] Motivating the study of these materials is the prediction of impressive mechanical properties such as hardness for allotropes like yne-diamond,^[10] which is composed of the hypothetical building block adamantyne. Although a variety of low molecular partial structures of these networks have been synthesized successfully, preparative access to these designer allotropes is still elusive.

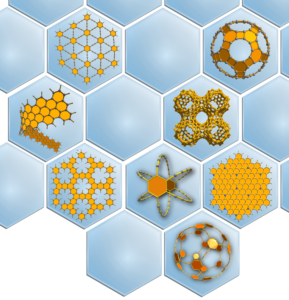
Because of the almost limitless possibilities of constructing both discrete and extended networks of sp-, sp²– and sp³-hybridized carbon atoms, many additional and so far unknown modifications with remarkable properties are imaginable and several examples have been predicted theoretically (Figure 3).

What makes synthetic carbon allotropes so attractive for chemists, physicists and materials scientists is not only the sheer multitude of aesthetically pleasing structures but, even more so, their outstanding and in many cases unprecedented properties. Common to fullerenes, carbon nanotubes, and graphene is the presence of fully conjugated π-electrons confined in either 0‑, quasi-1- or 2-dimensions. This leads to pronounced redox-activity and high electron mobilities accompanied by stability under ambient conditions.

Indeed, metallic carbon nanotubes and graphene are the first representatives of stable organic metals, where no further activation by doping or charge transfer is required to establish high charge-carrier mobilities. No other compound class surpasses fullerenes as electron acceptors in photovoltaic devices.^[11]

At the same time they exhibit remarkable biological properties such as anti-HIV-activity^[12] and the first example of metal-free superoxide dismutation, which is a major mechanism for efficient neuro-protection.^[13] Depending on their helicity, carbon nanotubes are either semiconducting or metallic. Both properties are very appealing for applications in the field of molecular electronics or for the refining of materials such as antistatic paints and shieldings. Their position as the record-holding mechanically strongest material makes them very attractive for reinforcing polymers in composite materials.

The specific properties of the youngest SCA representative graphene are considered to rank even higher. A distinct ambipolar field effect that indicates both excellent electron and hole conductivity has been measured in various analogously produced devices. These experiments indicate that the conductivity approaches the quantum limit (e²/h per carrier type) in undoped graphene when approaching zero gate voltage.^[14] The results are accompanied with a sudden reversal in the Hall coefficient. All other known materials inevitably traverse a metal/insulator transition at low temperatures, which is not observed for graphene down to 4K.^[15] An almost temperature-independent charge-carrier mobility up to µ = 230,000 cm²/Vs in suspended state and carrier concentrations of n = 2 x 10¹¹ translate into ballistic carrier transportation in the micrometer range.^[16] No other known material has yet been able to exhibit metallic conductivity at scales com­parable to those of single- or few-layer graphene. Another property that is so far unique to graphene is the ambient temperature quantum Hall effect.^[16c] Graphene’s intrinsic feature of being built from a single atomic layer naturally enables detection of single molecules adsorbed onto it, since even slight energetic shifts of the Fermi energy away from the Dirac point change conductivity dramatically.^[17] Usually the bulk nature of commonly used detectors lowers sensitivity and increases the S/N-ratio, resulting in detection thresholds that are not even close to those ex­hibited by graphene.

At a time when silicon-based technology is approaching its fundamental limits, any new candidate materials for future electronic devices is welcome. Owing to their spectacular electronic, optical, thermal, and mechanical properties, synthetic carbon allotropes are expected to offer an exceptional choice. Their importance is now abundantly clear in terms of fundamental physics.

References

[1] a) H. R. Karfunkel, T. Dressler, J. Am. Chem. Soc. 1992, 114, 2285-2288; b) F. Diederich, Y. Rubin, Angew. Chem. 1992, 104, 1123-1126.
[2] H. W. Kroto, J. R. Heath, S. C. O’Brien, R. F. Curl, R. E. Smalley, Nature 1985, 318, 162-163.
[3] W. Kraetschmer, L. D. Lamb, K. Fostiropoulos, D. R. Huffman, Nature 1990, 347, 354-358.
[4] A. Hirsch, Nature Mater. 2010, 9, 868-871.
[5] S. Iijima, Nature 1991, 354, 56-58.
[6] K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva, A. A. Firsov, Science 2004, 306, 666-669.
[7] A. Hirsch, M. Brettreich, Fullerenes – Chemistry and Reactions, Wiley-VCH, Weinheim, 2005.
[8] A. Hirsch, O. Vostrowsky, Top. Curr. Chem. 2005, 245, 193-237.
[9] a) U. H. F. Bunz, Y. Rubin, Y. Tobe, Chem. Soc. Rev. 1999, 28, 107-119; b) E. H. L. Falcao, F. Wudl, J. Chem. Technol. Biotechnol. 2007,
82, 524-531; c) F. Diederich, M. Kivala, Adv. Mater. 2010, 22, 803-812.
[10] L. Itzhaki, E. Altus, H. Basch, S. Hoz, Angew. Chem., Int. Ed. 2005, 44, 7432-7435.
[11] G. Dennler, M. C. Scharber, C. J. Brabec, Adv. Mater. 2009, 21, 1323-1338.
[12] S. H. Friedman, D. L. DeCamp, R. P. Sijbesma, G. Srdanov, F. Wudl, G. L. Kenyon, J. Am. Chem. Soc. 1993, 115, 6506-6509.
[13] G.-F. Liu, M. Filipovic, I. Ivanovic-Burmazovic, F. Beuerle, P. Witte, A. Hirsch, Angew. Chem., Int. Ed. 2008, 47, 3991-3994.
[14] K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, M. I. Katsnelson, I. V. Grigorieva, S. V. Dubonos, A. A. Firsov, Nature 2005, 438,
197-200.
[15] A. K. Geim, K. S. Novoselov, Nature Mater. 2007, 6, 183-191.
[16] a) K. S. Novoselov, Z. Jiang, Y. Zhang, S. V. Morozov, H. L. Stormer, U. Zeitler, J. C. Maan, G. S. Boebinger, P. Kim, A. K. Geim, Science
2007, 315, 1379; b) C. Berger, Z. Song, X. Li, X. Wu, N. Brown, C. Naud, D. Mayou, T. Li, J. Hass, A. N. Marchenkov, E. H. Conrad, P. N. First, W.
A. de Heer, Science 2006, 312, 1191-1196; c) Y. Zhang, Y.-W. Tan, H. L. Stormer, P. Kim, Nature 2005, 438, 201-204.
[17] S. Kim, J. Nah, I. Jo, D. Shahrjerdi, L. Colombo, Z. Yao, E. Tutuc, S. K. Banerjee, Appl. Phys. Lett. 2009, 94, 062107.

In order to fully exploit attractive applications such as nanoelectronics, sensors, nanocomposites, batteries, and supercapacitors a wide range of fundamental studies and discoveries into the science and technology of synthetic carbon allotropes is still required. It is clear that only an efficient interdisciplinary network of researchers with complementary expertise is the most appropriate tool to achieve important breakthroughs. The scientific aim of the SFB 953 ‘Synthetic Carbon Allotropes’ is to tackle these challenges by making use of the well-recognized expertise in Erlangen in the field of synthetic carbon allotropes through increasing the interactions between the disciplines within a formal environment. The joint effort and the interdisciplinary interaction between chemists, physicists, materials scientists, chemical engineers, and theoreticians forms the basis of our approach to these challenges.

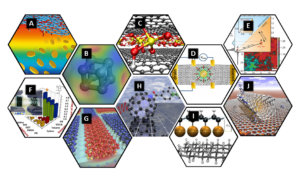
Our common twelve years goal is to develop and characterize an evolving family of carbon-based high-performance materials with tailored and tunable properties. The first funding period proved already to be very successful in targeting long-term goals (Fig. 4) such as: (a) the large scale production of single-layer graphene and carbon nanotubes with uniform helicity; (b) theory-guided design, synthesis, and characterization of new, so far elusive synthetic carbon allotropes and heterographenes; (c) theoretical prediction, experimental exploration, and comprehensive understanding of the covalent and non-covalent chemistry of carbon nanotubes, graphene, and of new, yet to be discovered forms of carbon; (d) comprehensive understanding of charge-transport as well as photoinduced and optical processes in nanoscale carbon systems; (e) development of novel tools for SCA characterization; (f) enabling carbon-allotrope-based solar cells as a sustainable energy resource for society; (g) development of high-performance devices such as semitransparent electrodes, low cost sensors, all-carbon integrated circuits, graphene THz emitters and transistors, and NIR emitters; (h) development of a self-sustainable hydrogen (H₂) generation system based on SWCNT- and graphene-carriers and coupled to a solar cell as energy source; (i) preparation of graphane and peralkylated graphene as the first family of 2-dimensional polymers, and (j) exploration of various families of inter-carbon-allotrope architectures.